エラトステネスの篩をJavaScriptで実装する
こんにちは。だいちゃんです。
shi3zさんのnote を読んでたら、最低限のプログラムの一例として**エラトステネスの篩(ふるい)**というアルゴリズムが登場していました。
調べてみると、プログラミングの題材としてもよく取り上げられる、指定した整数以下の素数を列挙するアルゴリズムらしかったので、力試しがてら、自分でも実装してみることにしました。
エラトステネスの篩
作成したのがこちら👆
適当な数字を入れて、開始をクリックするとアルゴリズムに従って素数以外をふるいにかけて、素数のみを列挙します。
普通に実装するだけだと、数秒で計算が終わってしまうところを、あえてインターバルを設けて少しずつ結果に近づく過程を見れるような仕組みにしたことが特徴です。
また、ビジュアル的にも、文字と図(?)を使って現時点でどういう判断となっているかを分かりやすくなるように工夫しました。
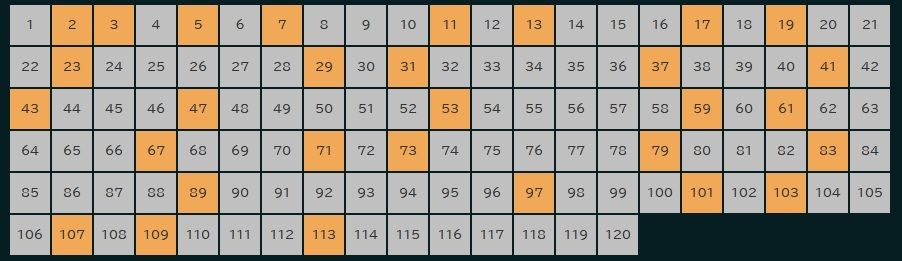
ちなみに、JavaScriptで計算してるため、あまりにも大きな数値をいれるとブラウザに負荷がかかりすぎてしまうので、入力できる数値は100,000までに制限しています。それでも実行環境によってはフリーズしたり、動作が重くなってしまうかもしれません。ご注意あれ~
アルゴリズム
ちゃんとした説明はWikipediaに譲るとして、簡単にアルゴリズムの概要だけ記載しておきます。
Step.1
任意の整数を入力します。この値を x とします。
開始ボタンがクリックされると、1からxまでの整数をずらっと並べておきます。このとき、すべての整数を true(未判定) (薄いオレンジ)とします。
Step.2
ずらっと並べた整数を頭から順に見ていって、true(未判定)(薄いオレンジ)になっている整数にぶち当たったら、次の処理を行います。
【1の場合】
1は素数ではないので false(素数ではない) にします。(グレーになります)
【2以上の場合】
その整数を prime(素数) にします。(濃いオレンジになります)
そして、その整数の2乗以上の倍数の値をすべて false(素数ではない) にします。(その整数は除く)
具体的には、次のような感じになります。
- 2の場合:2をprimeに。2の2乗は4なので、4以上の倍数(4, 6, 8, 10, 12, 14...)をfalseに。
- 3の場合:3をprimeに。3の2乗は9なので、9以上の倍数(9, 12, 15, 18, 21...)をfalseに。
- 4の場合:すでにfalseになってるのでスルー
- 5の場合:5をprimeに。5の2乗は25なので、25以上の倍数(25, 30, 35, 40...)をfalseに。
- 6の場合:すでにfalseになってるのでスルー
Step.3
xの平方根に達するまで Step.2 を繰り返す
Step.4
xの平方根に達した時点で true(未判定) になってる整数をすべて prime(素数) にします。
prime(素数) になっている整数がすべて素数です。
素数が出せたらこんな問題を解くプログラムもかけるみたい。力試し的には良さそう。
参考